Sebelum lebih jauh membahas bangun-bangun pada geometri bidang, akan diuraikan dulu pengertian titik, garis dan bidang dalam konsep geometri.
Titik dapat dibayangkan seperti bola yang semakin mengecil sehingga jari-jarinya nol. Titik dinyatakan dengan satu huruf besar (misalnya A, B, C dan sebagainya), dan karena tidak memiliki ukuran maka titik dikatakan berdimensi nol.
Garis dapat dibayangkan sebagai jejak titik yang bergerak lurus memanjang ke dua arah. Garis dinotasikan dengan huruf non-kapital (misalnya g, h, l dan sebagainya). Bidang dapat dibayangkan sebagai jejak garis yang bergerak menyamping tampa mengubah arah garis. Bidang meluas ke segala arah tanpa batas.
Selanjutnya akan dijelaskan beberapa definisi yang berhubungan dengan titik, garis dan bidang, yakni:
1. Ruas garis (segmen).
Ruas garis AB merupakan himpunan titik A, B dan semua titik diantara A dan B yang kolinier dengan garis melalui kedua titik tersebut.
2. Sinar (Ray).
Sinar AB merupakan himpunan semua titik pada ruas garis AB dan semua titik X yang segaris dengan A dan B sedemikian hingga B terletak diantara A dan X. Selanjutnya A dinamakan sebagai titik pangkal.
3. Sudut.
Sudut adalah gabungan dua sinar yang bersekutu dititik pangkalnya. Dua sinar ini dinamakan kaki sudut, sedangkan titik pangkal persekutuan dinamakan sebagai titik sudut..

Setelah mengetahui konsep-konsep dasar dalam geometri, berikut akan diuraikan konsep bangun geometri pada bidang.
Pada geometri bidang, bangun segibanyak (poligon ) merupakan bangun datar tertutup yang sisi-sisinya berupa ruas garis, dan setiap ruas garis hanya berpotongan pada ujung-ujungnya.,
Pada ilustrasi di atas, gambar 1, 2, 3 dan 4 merupakan poligon. Gambar 1 dan 2 disebut poligon konveks. Suatu bangun geometri dikatakan konveks jika setiap mengambil dua titik didalam poligon, maka seluruh ruas garis yang menghubungkannya berada di dalam bangun tersebut. Sementara itu gambar 3 dan 4 merupakan poligon konkaf. Dikatakan konkaf jika ada dua titik di dalam bangun, yang jika dihubungkan, maka terdapat bagian ruas garis yang berada di luar bangun. Gambar 5 dan 6 bukan poligon karena memiliki sisi yang bukan ruas garis.
Pada bab ini akan diuraikan lebih lanjut beberapa bangun dalam geometri bidang, yakni segi tiga, segi empat dan lingkaran
1. Segi tiga.
Segitiga adalah polygon dengan tiga sisi (dilambangkan dengan Δ ) dan merupakan gabungan tiga ruas garis yang ujung-ujungnya ditentukan oleh tiga titik tidak segaris. Ruas-ruas garis tersebut dinamakan sebagai sisi, sedangkan ketiga ujungnya dinamakan sebagai titik sudut.
Ketiga sisi pada segitiga tersebut harus memenuhi syarat ketaksamaan segitiga, yakni: Jika a, b dan c adalah sisi-sisi pada segitiga ABC, maka haruslah berlaku: a + b > c dan a + c > b dan b + c > a.
Berdasarkan besar sudutnya, segitiga dibagi menjadi 3 jenis, yaitu :
(1) Segitiga lancip, yakni segitiga yang semua sudutnya kurang dari 90o
(2) Segitiga siku-siku yakni segitiga yang salah satu sudutnya 90o
(3) Segitiga tumpul yakni segitiga yang salah satu sudutnya lebih dari 90o.
Berdasarkan panjang sisinya, segitiga dibedakan menjadi :
(1) segitiga samakaki yakni segitiga yang dua sisinya sama panjang
(2) segitiga samasisi yakni segitiga yang dua sisinya sama panjang
(3) Segitiga sembarang, yakni segitiga yang sisi-sisinya tidak ada yang sama panjang.
Dapat juga dikatakan, dua segitiga kongruen jika keenam unsur segitiga pertama kongruen dengan enam unsur yang bersesuaian pada segitiga yang kedua
Beberapa dalil dalam segitiga dapat diuraikan sebagai berikut :
Dalil 1
Dua segitiga kongruen jika ketiga sisi yang bersesuaian sama panjang
Contoh untuk dalil ini adalah:
Pada gambar berikut, AB dan CD saling membagi dua sama panjang di titik M. Jika AC = DB buktikan bahwa ΔAMC ≅ ΔDMB
Bukti:
Diketahui AB dan CD saling membagi dua sama panjang di M maka AM = BM dan CM = DM. Sementara itu diketahui bahwa AC = BD. Dengan demikian
berdasarkan postulat I kekongruenan, karena ketiga sisi yang bersesuaian sama panjang maka terbukti bahwa ΔAMC ≅ ΔDMB
Dalil 2.
Jika dua sisi dan sebuah sudut di antara keduanya pada suatu segitiga sama dengan dua sisi dan sudut di antaranya pada segitiga yang lain, maka kedua segitiga tersebut kongruen
Contoh untuk dalil ini adalah pada segitiga ABC disamping, dimana BM tegak lurus AC, dan M titik tengah AC. Maka ΔAMB ≅ ΔCMB
Bukti contoh ini adalah:
Diketahui M titik tengah AC, sehingga AM = CM dan AC tegak lurus BM. sehingga <AMB = <CMB = 90o.
Perhatikan segitiga AMB dan CMB, sisi MB digunakan pada kedua segitiga, sehingga MB = MB. Dari kedua segitiga di atas dipenuhi AM = CM, <AMB = <CMB , MB = MB sehingga, menurut dalil kekongruenan diatas terbukti bahwa ΔAMB ≅ ΔCMB
Dalil 3.
Jika dua sudut dan satu sisi di antara dua sudut pada suatu segitiga sama dengan dua sudut dan satu sisi di antara dua sudut pada segitiga yang lain, maka kedua segitiga tersebut kongruen.
Contoh untuk dalil ini adalah pada gambar segitiga ABC dan segitiga PQR diatas, dimana <A = <P, <C = <Q dan sisi AC = PQ maka berdasarkan dalil diatas berlaku ΔABC ≅ ΔPQR
Dua segitiga ABC dan PQR dikatakan sebangun (dilambangkan ΔABC ~ ΔPQR), jika ketiga sudut yang bersesuaian sama besar. Pada gambar dua segitiga dibawah ini berlaku : <A = <P, <B = <Q dan <C = <R. Sehingga ΔABC ~ ΔPQR
Suatu konsep yang berkaitan erat dengan kesebangunan adalah proporsi. Sifat proporsional pada segitiga ditunjukkan dengan dalil berikut ini.
Dalil 4.
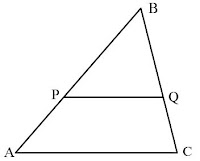
Suatu garis yang sejajar salah satu sisi segitiga dan memotong dua sisi yang lain membagi sisi-sisi tersebut secara proporsional.
Pada sebuah segitiga ABC, ditarik garis PQ sejajar AC. Jika garis PQ membagi BA dan BC sehingga panjang ruas garis yang bersesuaian pada setiap sisi memiliki perbandingan yang sama, yakni :
Selanjutnya akan dijelaskan garis-garis istimewa dalam segitiga, yakni garis sumbu, garis tinggi, garis berat dan garis bagi yakni sebagai berikut :
a. Garis sumbu suatu segitiga
Garis sumbu segitiga merupakan garis bagi tegak lurus setiap sisi segitiga tersebut.
Ketiga garis sumbu berpotongan di satu titik.
b. Garis tinggi suatu segitiga
Garis tinggi suatu segitiga merupakan garis yang melalui suatu titik sudut dan tegak lurus terhadap garis yang memuat sisi di depan sudut tersebut. Karena segitiga memiliki tiga titik sudut yang dapat dianggap sebagai puncak maka garis tinggi segitiga ada tiga buah.
Garis-garis tinggi suatu segitiga berpotongan di satu titik, yang disebut sebagai orthocenter.
c. Garis berat suatu segitiga
Garis berat adalah garis yang melalui titik sudut segitiga dan titik tengah sisi di depannya. Karena segitiga memiliki tiga sudut, maka terdapat tiga garis berat dalam sebuah segitiga. Ketiga garis berat ini berpotongan di satu titik yang disebut sebagai titik berat (centroid). Titik berat ini merupakan pusat kesetimbangan segitiga.
Jika sebuah segitiga digantungkan tepat pada titik beratnya, maka segitiga tersebut akan berada pada posisi horisontal.
d. Garis bagi sudut suatu segitiga
Garis bagi sudut segitiga adalah garis yang membagi sudut dalam suatu segitiga sehingga menjadi dua bagian yang sama besar.
Terdapat tiga garis bagi sudut suatu segitiga. Garis bagi sudut segitiga berpotongan di satu titik yang disebut incenter segitiga.
Titik ini merupakan titik pusat lingkaran dalam segitiga (lingkaran di dalam segitiga yang menyinggung semua sisinya).

Berikut ini akan diberikan beberapa contoh soal yang berkaitan dengan segi-tiga dan segi-empat yakni sebagai berikut:
2. Segi-empat
segiempat dapat didefinisikan sebagai poligon dengan empat sisi. Ada terdapat beberapa macam segi-empat, yakni sebagai berikut:
a. Jajar genjang (parallelogram)
Jajar genjang merupakan segi empat yang dua pasang sisi-sisi berhadapannya sejajar. Segi empat ABCD di samping merupakan jajar genjang karena AB sejajar DC dan AD sejajar BC
Pada jajar genjang ABCD, jika sisi AB dianggap sebagai alas, maka tinggi jajar genjang adalah DP, yakni jarak suatu titik pada sisi AB ke garis yang memuat sisi DC. Seperti halnya dalam segitiga, tinggi suatu jajar genjang tidak selalu harus dalam posisi vertikal.
Jajar genjang memiliki sifat-sifat:
1) Diagonal membagi jajar genjang menjadi dua segitiga kongruen.
2) Sudut-sudut yang berhadapan sama besar.
3) Sisi-sisi yang berhadapan sama panjang.
4). Sudut-sudut yang berdekatan saling berpelurus
5). Diagonal-diagonalnya saling membagi dua sama panjang
6) Luas jajar genjang dirumuskan : L = alas x tinggi
b. Persegi panjang
Persegi panjang adalah jajar genjang yang satu sudutnya siku-siku.
Berikut sifat-sifat persegi panjang:
1) Karena persegi panjang merupakan jajar genjang, maka semua sifat jajar genjang dimiliki oleh persegi panjang.
2) Keempat sudutnya sama besar (equiangular) dan berupa sudut siku-siku.
3) Diagonal persegi panjang sama panjang.
4) Luas persegi panjang dirumuskan :
Luas = panjang x lebar = AB x AD
c. Belah ketupat (rhombus)
Belah ketupat merupakan jajar genjang yang dua sisi berdekatannya sama panjang. Karena belah ketupat merupakan jajar genjang, maka semua sifat jajar genjang menjadi sifat belah ketupat.
Berikut ini beberapa sifat khusus belah ketupat.
1) Belah ketupat memiliki semua sifat jajar genjang.
2) Semua sisi belah ketupat mempunyai panjang yang sama (equilateral).
3) Diagonal-diagonal belah ketupat saling tegak lurus.
4) Diagonal-diagonal belah ketupat membagi dua sama besar sudut belah ketupat.
5) Luas belah ketupat dirumuskan :
L = alas x tinggi = AB x PD atau
L = ½ (diagonal1 x diagonal2) = ½ (AC x BD)
d. Persegi (square)
Persegi merupakan persegi panjang yang dua sisi berdekatannya sama panjang. Karena persegi merupakan kasus khusus dari persegi panjang dan persegi panjang merupakan kasus khusus dari jajar genjang maka persegi memiliki semua sifat persegi panjang dan sekaligus memiliki semua sifat jajar genjang.

Karena persegi memiliki dua sisi berdekatan yang sama panjang, maka persegi merupakan belah ketupat sehingga semua sifat belah ketupat juga dimiliki oleh persegi.
Persegi memiliki semua sifat jajargenjang, persegi panjang, dan belah ketupat.
e. Trapesium (trapezoid/trapezium)
trapesium merupakan segi empat yang mempunyai tepat sepasang sisi yang sejajar.
Jika AB sejajar CD dan AD tidak sejajar BC, maka segi empat ABCD merupakan trapesium.
Sisi AB dan CD disebut sisi-sisi sejajar atau sering juga disebut sisi alas (bases). Pasangan sisi yang tidak sejajar AD dan BC dinamakan kaki-kaki trapesium. Pasangan sudut yang menggunakan satu sisi sejajar sebagai kaki sudut bersama dinamakan pasangan sudut alas.
Trapesium sama kaki adalah trapesium yang kaki-kakinya sama panjang (AD = BC)
Sifat-sifat trapesium:
1) Masing-masing pasangan sudut berdekatan di antara dua sisi sejajar suatu trapesium saling berpelurus.
2) Pasangan sudut alas suatu trapesium samakaki sama besar.
3) Diagonal-diagonal trapesium sama kaki sama panjang.
4) Luas trapezium dirumuskan :
L = ½ (jumlah sisi-sisi sejajar x tinggi) = ½ (AB + DC)PD
g. Layang-layang (kite)
Layang-layang adalah segi empat konveks yang memiliki dua pasang sisi berdekatan yang kongruen, pasangan sisi kongruen yang satu berbeda dengan pasangan sisi kongruen yang lain.
Pada layang-layang diatas, diagonal BD membagi layang-layang menjadi dua segitiga yang kongruen. Diagonal AC membagi layang-layang menjadi dua segitiga samakaki yang tidak kongruen. <D dan <B yang dibentuk oleh dua sisi yang kongruen dinamakan sebagai sudut puncak (vertex angles) sedangkan <A dan <C adalah sudut bukan puncak (non vertex angles).
Layang-layang memiliki sifat:
1) Kedua sudut bukan puncak suatu layang-layang besarnya sama.
2) Diagonal-diagonal layang-layang saling tegak lurus.
3) Salah satu diagonal merupakan garis bagi diagonal yang lain.
4) Sudut puncak suatu layang-layang dibagi dua sama besar oleh diagonal yang melalui titik puncak.
Berikut ini akan diberikan beberapa contoh soal tentang segi-empat
3. Lingkaran
Lingkaran merupakan daerah yang dibatasi oleh titik-titik yang berjarak sama terhadap suatu titik tertentu. Titik tertentu ini disebut sebagai pusat lingkaran. Ruas garis yang menghubungkan suatu titik pada lingkaran ke pusat dinamakan jari-jari. Istilah jari-jari juga dapat digunakan untuk menyatakan panjang ruas garis yang menghubungkan pusat lingkaran dengan titik pada lingkaran.
Pada gambar di atas, garis lengkung BCD disebut busur pendek atau busur kecil, sedangkan garis lengkung BFD disebut busur panjang atau busur besar. Selanjutnya jika disebutkan busur BD maka yang dimaksud adalah busur pendek. Tali busur merupakan ruas garis yang menghubungkan dua titik pada lingkaran. Pada gambar, BF merupakan tali busur. Talibusur yang melalui pusat lingkaran dinamakan diameter.
Apotema suatu lingkaran merupakan ruas garis yang menghubungkan pusat lingkaran ke titik tengah tali busur. Istilah apotema dapat digunakan untuk menyatakan panjangnya. Sebagai contoh pada gambar di atas, ruas garis PQ, ataupun panjang PQ dapat disebut sebagai apotema. Apotema tegak lurus tali busur BF yang bersesuaian.
Tembereng merupakan daerah yang dibatasi oleh tali busur dan busurnya. Juring lingkaran merupakan daerah yang dibatasi oleh dua jari-jari dan busur. Perhatikan pada gambar di atas, bagian DPE yang diarsir merupakan juring kecil , dan bagian yang diarsir ABF merupakan tembereng lingkaran.
Untuk setiap lingkaran perbandingan dari keliling dan diameter selalu bernilai tetap yaitu mendekati 3,14. Nilai ini disebut sebagai π (dibaca “pi”). Sehingga berlaku :
maka diperoleh rumus Keliling lingkaran = 2 πr
Selanjutnya pada lingkaran berlaku pula perbandingan :
Luas lingkaran dapat dirumuskan sebagai :
L = π r2
Dengan r adalah panjang jari-jari lingkaran.
Pada gambar di atas titik P adalah pusat lingkaran, dan titik A, B, C, D, dan E terletak pada lingkaran. <CPD disebut sebagai sudut pusat dan <BAE dinamakan sudut keliling.
Perhatikan gambar di atas, <BPC merupakan sudut pusat, dan <BAC merupakan sudut keliling yang menghadap busur yang sama (busur BC).
Panjang AP = BP = CP, sehingga ΔAPB dan ΔAPC sama kaki serta berlaku <BAP = <ABP dan <CAP = <ACP.
Karena jumlah sudut segitiga 1800 maka pada ΔAPB berlaku <BPA = 180o – 2<BAP dan ΔAPC berlaku <APC = 180o – 2<CAP .
Sehingga :
<BPC = 360o – <BPA – <APC
<BPC = 360o – (180o – 2<BAP) – (180o – 2<CAP)
<BPC = 2(<BAP + CAP)
<BPC = 2<BAC
Jadi besar sudut pusat sama dengan dua kali besar sudut keliling yang menghadap busur yang sama.
Dari sifat ini dapat diturunkan sifat bahwa sudut-sudut keliling yang menghadap busur yang sama, akan selalu sama besar.
Sebagai bukti akan diperlihatkan pada gambar berikut :
Pada gambar lingkaran di atas, berlaku :
<BPC = 2<BDC ………. (1)
<BPC = 2<BAC ………..(2)
Dari (1) dan (2) terbukti bahwa
<BAC = <BDC
Garis singgung lingkaran adalah garis yang memotong lingkaran tepat di satu titik..
Garis singgung ini tegak lurus jari-jari yang melalui titik singgungnya.
Selanjutnya akan diberikan contoh-contoh soal tentang lingkaran, yakni sebagai berikut:
Titik dapat dibayangkan seperti bola yang semakin mengecil sehingga jari-jarinya nol. Titik dinyatakan dengan satu huruf besar (misalnya A, B, C dan sebagainya), dan karena tidak memiliki ukuran maka titik dikatakan berdimensi nol.
Garis dapat dibayangkan sebagai jejak titik yang bergerak lurus memanjang ke dua arah. Garis dinotasikan dengan huruf non-kapital (misalnya g, h, l dan sebagainya). Bidang dapat dibayangkan sebagai jejak garis yang bergerak menyamping tampa mengubah arah garis. Bidang meluas ke segala arah tanpa batas.
Selanjutnya akan dijelaskan beberapa definisi yang berhubungan dengan titik, garis dan bidang, yakni:
1. Ruas garis (segmen).
Ruas garis AB merupakan himpunan titik A, B dan semua titik diantara A dan B yang kolinier dengan garis melalui kedua titik tersebut.
2. Sinar (Ray).
Sinar AB merupakan himpunan semua titik pada ruas garis AB dan semua titik X yang segaris dengan A dan B sedemikian hingga B terletak diantara A dan X. Selanjutnya A dinamakan sebagai titik pangkal.
3. Sudut.
Sudut adalah gabungan dua sinar yang bersekutu dititik pangkalnya. Dua sinar ini dinamakan kaki sudut, sedangkan titik pangkal persekutuan dinamakan sebagai titik sudut..

Setelah mengetahui konsep-konsep dasar dalam geometri, berikut akan diuraikan konsep bangun geometri pada bidang.
Pada geometri bidang, bangun segibanyak (poligon ) merupakan bangun datar tertutup yang sisi-sisinya berupa ruas garis, dan setiap ruas garis hanya berpotongan pada ujung-ujungnya.,
Pada ilustrasi di atas, gambar 1, 2, 3 dan 4 merupakan poligon. Gambar 1 dan 2 disebut poligon konveks. Suatu bangun geometri dikatakan konveks jika setiap mengambil dua titik didalam poligon, maka seluruh ruas garis yang menghubungkannya berada di dalam bangun tersebut. Sementara itu gambar 3 dan 4 merupakan poligon konkaf. Dikatakan konkaf jika ada dua titik di dalam bangun, yang jika dihubungkan, maka terdapat bagian ruas garis yang berada di luar bangun. Gambar 5 dan 6 bukan poligon karena memiliki sisi yang bukan ruas garis.
Pada bab ini akan diuraikan lebih lanjut beberapa bangun dalam geometri bidang, yakni segi tiga, segi empat dan lingkaran
1. Segi tiga.
Segitiga adalah polygon dengan tiga sisi (dilambangkan dengan Δ ) dan merupakan gabungan tiga ruas garis yang ujung-ujungnya ditentukan oleh tiga titik tidak segaris. Ruas-ruas garis tersebut dinamakan sebagai sisi, sedangkan ketiga ujungnya dinamakan sebagai titik sudut.
Ketiga sisi pada segitiga tersebut harus memenuhi syarat ketaksamaan segitiga, yakni: Jika a, b dan c adalah sisi-sisi pada segitiga ABC, maka haruslah berlaku: a + b > c dan a + c > b dan b + c > a.
Berdasarkan besar sudutnya, segitiga dibagi menjadi 3 jenis, yaitu :
(1) Segitiga lancip, yakni segitiga yang semua sudutnya kurang dari 90o
(2) Segitiga siku-siku yakni segitiga yang salah satu sudutnya 90o
(3) Segitiga tumpul yakni segitiga yang salah satu sudutnya lebih dari 90o.
Berdasarkan panjang sisinya, segitiga dibedakan menjadi :
(1) segitiga samakaki yakni segitiga yang dua sisinya sama panjang
(2) segitiga samasisi yakni segitiga yang dua sisinya sama panjang
(3) Segitiga sembarang, yakni segitiga yang sisi-sisinya tidak ada yang sama panjang.
Beberapa dalil dalam segitiga dapat diuraikan sebagai berikut :
Dalil 1
Dua segitiga kongruen jika ketiga sisi yang bersesuaian sama panjang
Contoh untuk dalil ini adalah:
Pada gambar berikut, AB dan CD saling membagi dua sama panjang di titik M. Jika AC = DB buktikan bahwa ΔAMC ≅ ΔDMB
Bukti:
Diketahui AB dan CD saling membagi dua sama panjang di M maka AM = BM dan CM = DM. Sementara itu diketahui bahwa AC = BD. Dengan demikian
berdasarkan postulat I kekongruenan, karena ketiga sisi yang bersesuaian sama panjang maka terbukti bahwa ΔAMC ≅ ΔDMB
Dalil 2.
Jika dua sisi dan sebuah sudut di antara keduanya pada suatu segitiga sama dengan dua sisi dan sudut di antaranya pada segitiga yang lain, maka kedua segitiga tersebut kongruen
Contoh untuk dalil ini adalah pada segitiga ABC disamping, dimana BM tegak lurus AC, dan M titik tengah AC. Maka ΔAMB ≅ ΔCMB
Bukti contoh ini adalah:
Diketahui M titik tengah AC, sehingga AM = CM dan AC tegak lurus BM. sehingga <AMB = <CMB = 90o.
Perhatikan segitiga AMB dan CMB, sisi MB digunakan pada kedua segitiga, sehingga MB = MB. Dari kedua segitiga di atas dipenuhi AM = CM, <AMB = <CMB , MB = MB sehingga, menurut dalil kekongruenan diatas terbukti bahwa ΔAMB ≅ ΔCMB
Dalil 3.
Jika dua sudut dan satu sisi di antara dua sudut pada suatu segitiga sama dengan dua sudut dan satu sisi di antara dua sudut pada segitiga yang lain, maka kedua segitiga tersebut kongruen.
Contoh untuk dalil ini adalah pada gambar segitiga ABC dan segitiga PQR diatas, dimana <A = <P, <C = <Q dan sisi AC = PQ maka berdasarkan dalil diatas berlaku ΔABC ≅ ΔPQR
Dua segitiga ABC dan PQR dikatakan sebangun (dilambangkan ΔABC ~ ΔPQR), jika ketiga sudut yang bersesuaian sama besar. Pada gambar dua segitiga dibawah ini berlaku : <A = <P, <B = <Q dan <C = <R. Sehingga ΔABC ~ ΔPQR
Suatu konsep yang berkaitan erat dengan kesebangunan adalah proporsi. Sifat proporsional pada segitiga ditunjukkan dengan dalil berikut ini.
Dalil 4.
Suatu garis yang sejajar salah satu sisi segitiga dan memotong dua sisi yang lain membagi sisi-sisi tersebut secara proporsional.
Pada sebuah segitiga ABC, ditarik garis PQ sejajar AC. Jika garis PQ membagi BA dan BC sehingga panjang ruas garis yang bersesuaian pada setiap sisi memiliki perbandingan yang sama, yakni :
Selanjutnya akan dijelaskan garis-garis istimewa dalam segitiga, yakni garis sumbu, garis tinggi, garis berat dan garis bagi yakni sebagai berikut :
a. Garis sumbu suatu segitiga
Garis sumbu segitiga merupakan garis bagi tegak lurus setiap sisi segitiga tersebut.
Ketiga garis sumbu berpotongan di satu titik.
b. Garis tinggi suatu segitiga
Garis tinggi suatu segitiga merupakan garis yang melalui suatu titik sudut dan tegak lurus terhadap garis yang memuat sisi di depan sudut tersebut. Karena segitiga memiliki tiga titik sudut yang dapat dianggap sebagai puncak maka garis tinggi segitiga ada tiga buah.
Garis-garis tinggi suatu segitiga berpotongan di satu titik, yang disebut sebagai orthocenter.
c. Garis berat suatu segitiga
Garis berat adalah garis yang melalui titik sudut segitiga dan titik tengah sisi di depannya. Karena segitiga memiliki tiga sudut, maka terdapat tiga garis berat dalam sebuah segitiga. Ketiga garis berat ini berpotongan di satu titik yang disebut sebagai titik berat (centroid). Titik berat ini merupakan pusat kesetimbangan segitiga.
Jika sebuah segitiga digantungkan tepat pada titik beratnya, maka segitiga tersebut akan berada pada posisi horisontal.
Garis bagi sudut segitiga adalah garis yang membagi sudut dalam suatu segitiga sehingga menjadi dua bagian yang sama besar.
Terdapat tiga garis bagi sudut suatu segitiga. Garis bagi sudut segitiga berpotongan di satu titik yang disebut incenter segitiga.
Titik ini merupakan titik pusat lingkaran dalam segitiga (lingkaran di dalam segitiga yang menyinggung semua sisinya).

Berikut ini akan diberikan beberapa contoh soal yang berkaitan dengan segi-tiga dan segi-empat yakni sebagai berikut:
2. Segi-empat
segiempat dapat didefinisikan sebagai poligon dengan empat sisi. Ada terdapat beberapa macam segi-empat, yakni sebagai berikut:
a. Jajar genjang (parallelogram)
Jajar genjang merupakan segi empat yang dua pasang sisi-sisi berhadapannya sejajar. Segi empat ABCD di samping merupakan jajar genjang karena AB sejajar DC dan AD sejajar BC
Pada jajar genjang ABCD, jika sisi AB dianggap sebagai alas, maka tinggi jajar genjang adalah DP, yakni jarak suatu titik pada sisi AB ke garis yang memuat sisi DC. Seperti halnya dalam segitiga, tinggi suatu jajar genjang tidak selalu harus dalam posisi vertikal.
Jajar genjang memiliki sifat-sifat:
1) Diagonal membagi jajar genjang menjadi dua segitiga kongruen.
2) Sudut-sudut yang berhadapan sama besar.
3) Sisi-sisi yang berhadapan sama panjang.
4). Sudut-sudut yang berdekatan saling berpelurus
5). Diagonal-diagonalnya saling membagi dua sama panjang
6) Luas jajar genjang dirumuskan : L = alas x tinggi
b. Persegi panjang
Persegi panjang adalah jajar genjang yang satu sudutnya siku-siku.
Berikut sifat-sifat persegi panjang:
1) Karena persegi panjang merupakan jajar genjang, maka semua sifat jajar genjang dimiliki oleh persegi panjang.
2) Keempat sudutnya sama besar (equiangular) dan berupa sudut siku-siku.
3) Diagonal persegi panjang sama panjang.
4) Luas persegi panjang dirumuskan :
Luas = panjang x lebar = AB x AD
c. Belah ketupat (rhombus)
Belah ketupat merupakan jajar genjang yang dua sisi berdekatannya sama panjang. Karena belah ketupat merupakan jajar genjang, maka semua sifat jajar genjang menjadi sifat belah ketupat.
Berikut ini beberapa sifat khusus belah ketupat.
1) Belah ketupat memiliki semua sifat jajar genjang.
2) Semua sisi belah ketupat mempunyai panjang yang sama (equilateral).
3) Diagonal-diagonal belah ketupat saling tegak lurus.
4) Diagonal-diagonal belah ketupat membagi dua sama besar sudut belah ketupat.
5) Luas belah ketupat dirumuskan :
L = alas x tinggi = AB x PD atau
L = ½ (diagonal1 x diagonal2) = ½ (AC x BD)
d. Persegi (square)
Persegi merupakan persegi panjang yang dua sisi berdekatannya sama panjang. Karena persegi merupakan kasus khusus dari persegi panjang dan persegi panjang merupakan kasus khusus dari jajar genjang maka persegi memiliki semua sifat persegi panjang dan sekaligus memiliki semua sifat jajar genjang.

Karena persegi memiliki dua sisi berdekatan yang sama panjang, maka persegi merupakan belah ketupat sehingga semua sifat belah ketupat juga dimiliki oleh persegi.
Persegi memiliki semua sifat jajargenjang, persegi panjang, dan belah ketupat.
e. Trapesium (trapezoid/trapezium)
trapesium merupakan segi empat yang mempunyai tepat sepasang sisi yang sejajar.
Jika AB sejajar CD dan AD tidak sejajar BC, maka segi empat ABCD merupakan trapesium.
Sisi AB dan CD disebut sisi-sisi sejajar atau sering juga disebut sisi alas (bases). Pasangan sisi yang tidak sejajar AD dan BC dinamakan kaki-kaki trapesium. Pasangan sudut yang menggunakan satu sisi sejajar sebagai kaki sudut bersama dinamakan pasangan sudut alas.
Trapesium sama kaki adalah trapesium yang kaki-kakinya sama panjang (AD = BC)
Sifat-sifat trapesium:
1) Masing-masing pasangan sudut berdekatan di antara dua sisi sejajar suatu trapesium saling berpelurus.
2) Pasangan sudut alas suatu trapesium samakaki sama besar.
3) Diagonal-diagonal trapesium sama kaki sama panjang.
4) Luas trapezium dirumuskan :
L = ½ (jumlah sisi-sisi sejajar x tinggi) = ½ (AB + DC)PD
g. Layang-layang (kite)
Layang-layang adalah segi empat konveks yang memiliki dua pasang sisi berdekatan yang kongruen, pasangan sisi kongruen yang satu berbeda dengan pasangan sisi kongruen yang lain.
Pada layang-layang diatas, diagonal BD membagi layang-layang menjadi dua segitiga yang kongruen. Diagonal AC membagi layang-layang menjadi dua segitiga samakaki yang tidak kongruen. <D dan <B yang dibentuk oleh dua sisi yang kongruen dinamakan sebagai sudut puncak (vertex angles) sedangkan <A dan <C adalah sudut bukan puncak (non vertex angles).
Layang-layang memiliki sifat:
1) Kedua sudut bukan puncak suatu layang-layang besarnya sama.
2) Diagonal-diagonal layang-layang saling tegak lurus.
3) Salah satu diagonal merupakan garis bagi diagonal yang lain.
4) Sudut puncak suatu layang-layang dibagi dua sama besar oleh diagonal yang melalui titik puncak.
Berikut ini akan diberikan beberapa contoh soal tentang segi-empat
3. Lingkaran
Lingkaran merupakan daerah yang dibatasi oleh titik-titik yang berjarak sama terhadap suatu titik tertentu. Titik tertentu ini disebut sebagai pusat lingkaran. Ruas garis yang menghubungkan suatu titik pada lingkaran ke pusat dinamakan jari-jari. Istilah jari-jari juga dapat digunakan untuk menyatakan panjang ruas garis yang menghubungkan pusat lingkaran dengan titik pada lingkaran.
Pada gambar di atas, garis lengkung BCD disebut busur pendek atau busur kecil, sedangkan garis lengkung BFD disebut busur panjang atau busur besar. Selanjutnya jika disebutkan busur BD maka yang dimaksud adalah busur pendek. Tali busur merupakan ruas garis yang menghubungkan dua titik pada lingkaran. Pada gambar, BF merupakan tali busur. Talibusur yang melalui pusat lingkaran dinamakan diameter.
Apotema suatu lingkaran merupakan ruas garis yang menghubungkan pusat lingkaran ke titik tengah tali busur. Istilah apotema dapat digunakan untuk menyatakan panjangnya. Sebagai contoh pada gambar di atas, ruas garis PQ, ataupun panjang PQ dapat disebut sebagai apotema. Apotema tegak lurus tali busur BF yang bersesuaian.
Tembereng merupakan daerah yang dibatasi oleh tali busur dan busurnya. Juring lingkaran merupakan daerah yang dibatasi oleh dua jari-jari dan busur. Perhatikan pada gambar di atas, bagian DPE yang diarsir merupakan juring kecil , dan bagian yang diarsir ABF merupakan tembereng lingkaran.
Untuk setiap lingkaran perbandingan dari keliling dan diameter selalu bernilai tetap yaitu mendekati 3,14. Nilai ini disebut sebagai π (dibaca “pi”). Sehingga berlaku :
maka diperoleh rumus Keliling lingkaran = 2 πr
Selanjutnya pada lingkaran berlaku pula perbandingan :
Luas lingkaran dapat dirumuskan sebagai :
L = π r2
Dengan r adalah panjang jari-jari lingkaran.
Pada gambar di atas titik P adalah pusat lingkaran, dan titik A, B, C, D, dan E terletak pada lingkaran. <CPD disebut sebagai sudut pusat dan <BAE dinamakan sudut keliling.
Perhatikan gambar di atas, <BPC merupakan sudut pusat, dan <BAC merupakan sudut keliling yang menghadap busur yang sama (busur BC).
Panjang AP = BP = CP, sehingga ΔAPB dan ΔAPC sama kaki serta berlaku <BAP = <ABP dan <CAP = <ACP.
Karena jumlah sudut segitiga 1800 maka pada ΔAPB berlaku <BPA = 180o – 2<BAP dan ΔAPC berlaku <APC = 180o – 2<CAP .
Sehingga :
<BPC = 360o – <BPA – <APC
<BPC = 360o – (180o – 2<BAP) – (180o – 2<CAP)
<BPC = 2(<BAP + CAP)
<BPC = 2<BAC
Jadi besar sudut pusat sama dengan dua kali besar sudut keliling yang menghadap busur yang sama.
Dari sifat ini dapat diturunkan sifat bahwa sudut-sudut keliling yang menghadap busur yang sama, akan selalu sama besar.
Sebagai bukti akan diperlihatkan pada gambar berikut :
Pada gambar lingkaran di atas, berlaku :
<BPC = 2<BDC ………. (1)
<BPC = 2<BAC ………..(2)
Dari (1) dan (2) terbukti bahwa
<BAC = <BDC
Garis singgung lingkaran adalah garis yang memotong lingkaran tepat di satu titik..
Garis singgung ini tegak lurus jari-jari yang melalui titik singgungnya.
Selanjutnya akan diberikan contoh-contoh soal tentang lingkaran, yakni sebagai berikut:




























0 komentar
Posting Komentar