Jika u(x) dan v(x) adalah fungsi-fungsi yang terdefinisi pada bilangan real, dan u‟(x) dan v‟(x) adalah turunannya, maka kita dapat menurunkan rumus turunan hasil kali, hasil bagi dua fungsi dan pemangkatan fungsi, yakni sebagai berikut:
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
01. Tentukanlah turunan dari setiap fungsi aljabar berikut ini :
(a) f(x) = (x2 – 4x)(2x + 3)
(b) f(x) = (2x2 + 3x – 5)(4x – 2)
Jawab
(a) f(x) = (x2 – 4x)(2x + 3)
Misalkan
u = x2 – 4x maka u' = 2x
v = 2x + 3 maka v' = 2
maka
f '(x) = u'.v + u.v'
f '(x) = (2x)(2x + 3) + (x2 – 4x)(2)
f '(x) = 2x2 + 6x + 2x2 – 8x
f '(x) = 4x2 – 2x
(b) f(x) = (2x2 + 3x – 5)(4x – 2)
Misalkan
u = 2x2 + 3x – 5 maka u' = 4x + 3
v = 4x – 2 maka v' = 4
maka
f '(x) = u'.v + u.v'
f '(x) = (4x + 3)(4x – 2) + (2x2 + 3x – 5)(4)
f '(x) = 16x2 – 8x + 12x – 6 + 8x2 + 12x – 20
f '(x) = 24x2 + 16x – 26
02. Tentukanlah turunan dari setiap fungsi aljabar berikut ini
Jawab
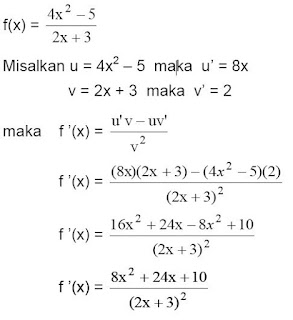
03. Tentukanlah turunan dari setiap fungsi aljabar berikut ini :
f(x) = 3(2x + 4)5
Jawab
f(x) = 3(2x + 4)5
Misalkan u = 2x + 4 maka u' = 2
Jadi f (x) = 3u5
f '(x) = 15u4.u'
f '(x) = 15(2x + 4)4(2)
f '(x) = 30(2x + 4)4
Disamping ketiga aturan di atas, terdapat juga aturan rantai untuk menentukan turunan pemangkatan fungsi. Aturan ini mengambil dasar dari notasi Leibniz untuk turunan, sebagai berikut :
Misalkan f, g dan h adalah fungsi-fungsi yang terdefinisi pada x bilangan real, sehingga jika y = f { g(x) } maka aturan rantai untuk turunan fungsi y terhadap x adalah :
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
04. Dengan aturan rantai, tentukanlah turunan setiap fungsi berikut ini
y = 3(x2 - 6x + 8)5
Jawab
Selain itu, ada juga turunan pertama, kedua, dan seterusnya. Penjelasannya sebagai berikut.
Untuk lebih jelasnya, ikutilah contoh soal berikut ini
05. Tentukanlah nilai turunan kedua dari setiap fungsi berikut ini untuk setiap nilai x yang diberikan
(a) f(x) = 2x3 –7x2 – 4x + 8
untuk x = 5
Jawab
f(x) = 2x3 –7x2 – 4x + 8
maka
f '(x) = 6x2 – 14x – 4
f ''(x) = 12x – 14
Sehingga :
f ''(5) = 12(5) – 14
f '‟(2) = 60 – 14
f '‟(2) = 46
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
01. Tentukanlah turunan dari setiap fungsi aljabar berikut ini :
(a) f(x) = (x2 – 4x)(2x + 3)
(b) f(x) = (2x2 + 3x – 5)(4x – 2)
Jawab
(a) f(x) = (x2 – 4x)(2x + 3)
Misalkan
u = x2 – 4x maka u' = 2x
v = 2x + 3 maka v' = 2
maka
f '(x) = u'.v + u.v'
f '(x) = (2x)(2x + 3) + (x2 – 4x)(2)
f '(x) = 2x2 + 6x + 2x2 – 8x
f '(x) = 4x2 – 2x
(b) f(x) = (2x2 + 3x – 5)(4x – 2)
Misalkan
u = 2x2 + 3x – 5 maka u' = 4x + 3
v = 4x – 2 maka v' = 4
maka
f '(x) = u'.v + u.v'
f '(x) = (4x + 3)(4x – 2) + (2x2 + 3x – 5)(4)
f '(x) = 16x2 – 8x + 12x – 6 + 8x2 + 12x – 20
f '(x) = 24x2 + 16x – 26
02. Tentukanlah turunan dari setiap fungsi aljabar berikut ini
Jawab
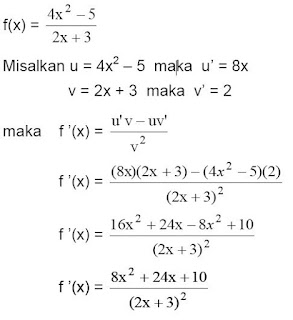
03. Tentukanlah turunan dari setiap fungsi aljabar berikut ini :
f(x) = 3(2x + 4)5
Jawab
f(x) = 3(2x + 4)5
Misalkan u = 2x + 4 maka u' = 2
Jadi f (x) = 3u5
f '(x) = 15u4.u'
f '(x) = 15(2x + 4)4(2)
f '(x) = 30(2x + 4)4
Disamping ketiga aturan di atas, terdapat juga aturan rantai untuk menentukan turunan pemangkatan fungsi. Aturan ini mengambil dasar dari notasi Leibniz untuk turunan, sebagai berikut :
Misalkan f, g dan h adalah fungsi-fungsi yang terdefinisi pada x bilangan real, sehingga jika y = f { g(x) } maka aturan rantai untuk turunan fungsi y terhadap x adalah :
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
04. Dengan aturan rantai, tentukanlah turunan setiap fungsi berikut ini
y = 3(x2 - 6x + 8)5
Jawab
Untuk lebih jelasnya, ikutilah contoh soal berikut ini
05. Tentukanlah nilai turunan kedua dari setiap fungsi berikut ini untuk setiap nilai x yang diberikan
(a) f(x) = 2x3 –7x2 – 4x + 8
untuk x = 5
Jawab
f(x) = 2x3 –7x2 – 4x + 8
maka
f '(x) = 6x2 – 14x – 4
f ''(x) = 12x – 14
Sehingga :
f ''(5) = 12(5) – 14
f '‟(2) = 60 – 14
f '‟(2) = 46






jawaban soal 1a kanyaknya salah
BalasHapus